To make predictions about events, concepts, or phenomena, researchers must perform detailed, objective analyses. One procedure to use in such analyses is a census, in which every member of the population is studied. Conducting a census for each research project is impractical, however, and researchers must resort to alternative methods. The most widely used alternative is to select a random sample from the population, examine it, and make predictions from it that can be generalized to the population. There are several procedures for identifying the units that are to compose a random sample.

 

If the scientific procedure is to provide valid and useful results, researchers must pay close attention to the methods they use in selecting a sample. This chapter will describe several types of samples commonly used in mass media research. Some are elementary and do not require a great deal of time or resources. Other sampling methods entail great expense and time. Researchers must decide whether costs and time are justified in relation to the results generated.

 

Sampling procedures must not be taken lightly in the process of scientific investigation. It makes no sense to develop a research design for testing a valuable hypothesis or research question and then nullify this effort by neglecting correct sampling procedures. These procedures must be continually scrutinized to ensure that the results of an analysis are not sample-specific; that is, results are not based on the type of sample used in the study.

 

This chapter describes the basics of the sampling methods that are widely used in research. However, considering that sampling theory has become a distinct discipline in itself, there are some studies, such as nationwide surveys, that require a consultation of more technical discussions of sampling. 

 

3.1 Population and Sample

 

One goal of scientific research is to describe the nature of a population, that is, a group or class of subjects, variables, concepts, or phenomena. In some cases this is achieved through the investigation of an entire class or group, such as a study of prime-time television programs during the week of September 10 — 16. The process of examining every member of such a population is called a census. In many situations, however, the chance of investigating an entire population is remote, if not nonexistent, due to time and resource constraints. Studying every member of a population is also generally cost prohibitive, and may in fact confound the research because measurements of large numbers of people often affect measurement quality.

 

The usual procedure in these instances is to select a sample from the population. A sample is a subset of the population that is taken to be representative of the entire population. An important word in this definition is representative. A sample that is not representative of the population, regardless of its size, is inadequate for testing purposes: the results cannot be generalized.

 

3.2 Probability and Nonprobability Samples 

 

A probability sample is selected according to mathematical guidelines whereby the chance for selection of each unit is known. A nonprobability sample does not follow the guidelines of mathematical probability. However, the most significant characteristic distinguishing the two types of samples is that probability sampling allows researchers to calculate the amount of sampling error present in a research study; non-probability sampling does not.

 

In deciding whether to use a probability or a nonprobability sample, a researcher should consider four points.

 

1. Purpose of the study: Some research studies are not designed for generalization to the population, but rather to investigate variable relationships or to collect exploratory data for designing questionnaires or measurement instruments. A nonprobability sample is often appropriate in situations of these types.

 

2. Cost versus value: The sample should produce the greatest value for the least investment. If the cost of a probability sample is too high in relation to the type and quality of information collected, a nonprobability sample is a possible alternative.

 

3. Time constraints: In many cases researchers collecting preliminary information operate under time constraints imposed by sponsoring agencies, management directives, or publication guidelines. Since probability sampling is often time-consuming, a non-probability sample may provide temporary relief.

 

4. Amount of error allowed: In preliminary or pilot studies, where error control is not a prime concern, a nonprobability sample is usually adequate.

 

Probability sampling generally incorporates some type of systematic selection procedure, such as a table of random numbers, to ensure that each unit has an equal chance of being selected. However, it does not always guarantee a representative sample from the population, even when systematic selection is followed. It is possible to randomly select 50 members of the student body at a university in order to determine the average height of all students enrolled and, by extraordinary coincidence, end up with 50 candidates for the basketball team. Such an event is unlikely, but it is possible, and this possibility underscores the need to replicate any study.

3.3.  Types of Nonprobability Samples

 

Nonprobability sampling is frequently used in mass media research, particularly in the form of available samples, samples using volunteer subjects, and purposive samples. Mall intercepts use nonprobability sampling. An available sample (also known as convenience sample) is a collection of readily accessible subjects for study, such as a group of students enrolled in an introductory mass media course, or shoppers in a mall. Although available samples can be helpful in collecting exploratory information and may produce useful data in some instances, the samples are problematic because they contain unknown quantities of error. Researchers need to consider the positive and negative qualities of available samples before using them in a research study.

 

Available samples are a subject of heated debate in many research fields. Critics argue that regardless, of the results they may generate, available samples do not represent the population and therefore have no external validity.

Proponents of the available sample procedure claim that if a phenomenon, characteristic, or trait does in fact exist, it should exist in any sample. In addition, some scholars have contested the very notion of sample representativeness.

 

Available samples can be useful in pretesting questionnaires or other preliminary (pilot study) work. They often help eliminate potential problems in research procedures, testing, and methodology before the final research study is attempted.

 

Subjects who constitute a volunteer sample also form a nonprobability sample, since the individuals are not selected mathematically. There is concern in all areas of research with regard to persons who willingly participate in research projects; these subjects differ greatly from non-volunteers and may consequently produce erroneous research results. The characteristics of volunteer subjects can be defined on the basis of several studies and found that such subjects, in comparison with nonvolunteers, tend to exhibit higher educational levels, higher occupational status, greater need for approval, higher intelligence, and lower authoritarianism. They also seem to be more sociable, more "arousal-seeking," and more unconventional; they are more likely to be first children, and they are generally younger.

 

These characteristics mean that the use of volunteer subjects may significantly bias the results of a research study and may lead to inaccurate estimates of various population parameters. Also, available data seem to indicate that volunteers may, more often than nonvolunteers, provide data to support a researcher's hypothesis. In some cases volunteer subjects are necessary—for example, in comparison tests of products or services. However, volunteers should be used with caution because, as with available samples, there is an unknown quantity of error present in the data.

 

Although volunteer samples have been shown to be inappropriate in scientific research, the electronic media have begun to legitimize volunteers through the various polls conducted on radio and television stations, and the television networks. Local television news programs, for example, often report the results of the latest "viewer poll" about some local concern. Even though announcers occasionally say that the polls are not intended to be scientific in nature, the results are presented as such. Unwary listeners and viewers are being conned by the media. Such telephone polls are disturbing to legitimate scientific researchers.

 

A purposive sample includes subjects selected on the basis of specific characteristics or qualities and eliminates those who fail to meet these criteria. Purposive samples are often used in advertising studies: researchers select subjects who use a particular type of product and ask them to compare it with a new product. A purposive sample is chosen with the knowledge that it is not representative of the general population; rather it attempts to represent a specific portion of the population. In a similar method, the quota sample, subjects are selected to meet a predetermined or known percentage. For example, a researcher interested in finding out how VCR owners differ in their use of television from non-VCR-owners may know that 10% of a particular population owns a VCR. The sample the researcher selected, therefore, would be composed of 10% of VCR owners and 90% non-VCR-owners (to reflect the population characteristics).

 

Another nonprobability sampling method is to select subjects haphazardly on the basis of appearance or convenience, or because they seem to meet certain requirements (the subjects look educated). Haphazard selection involves researcher subjectivity and introduces error. Some haphazard samples give the illusion of a probability sample; these must be carefully approached. For example, interviewing every 10th person who walks by in a shopping center is haphazard, since not everyone in the population has an equal chance of walking by that particular location. Some people live across town, some shop in other centers, and so on.

Some researchers, research suppliers, and field services try to work around the problems associated with convenience samples in mall intercepts by using a procedure based on what is called "The Law of Large Numbers." Essentially, the researchers interview thousands of respondents instead of hundreds. The presumption (and sales approach used on clients) is that the large number of respondents eliminates the problems of convenience sampling. It does not. The large number approach is still a convenience sample. It is not a random sample as described in the first sentence of the next section.

3.4  Types of Probability Sample

 

3.4.1 Simple Random Sample

 

The most basic type of probability sampling is the simple random sample, where each subject or unit in the population has an equal chance of being selected. If a subject or unit is drawn from the population and removed from subsequent selections, the procedure is known as random sampling without replacement — the most widely used random sampling method. Random sampling with replacement involves returning the subject or unit into the population so that it has a chance of being chosen another time. Sampling with replacement is often used in more complicated research studies such as nationwide surveys.

 

Researchers usually use a table of random numbers to generate a simple random sample. For example, a researcher, who wants to analyze 10 prime-time television programs out of a total population of 100 programs to determine how the medium portrays elderly people, can take a random sample from the 100 programs by numbering each show from 00 to 99 and then selecting 10 numbers from a table of random numbers. First, a starting point in the table is selected at random. There is no specific way to choose a starting point; it is an arbitrary decision. The researcher then selects the remaining 9 numbers by going up, down, left, or right on the table — or even randomly throughout the table. For example, if it is decided to go down in the table from the starting point 44 until a sample of 10 has been drawn, the sample would include television programs numbered 44, 85, 46, 71, 17, 50, 66, 56, 03, and 49.

 

Simple random samples for use in telephone surveys are often obtained by a process called random digit dialing. One method involves randomly selecting four-digit numbers (usually generated by a computer or through the use of a random numbers table) and adding them to the three-digit exchange prefixes in the city in which the survey is conducted. A single four-digit series may be used once, or it may be added to all the prefixes.

 

Unfortunately, a large number of the telephone numbers generated by this method of random digit dialing are invalid because some phones have been disconnected, some numbers generated have not yet been assigned, and for other reasons. Therefore, it is advisable to produce at least three times the number of telephone numbers needed; if a sample of 100 is required, at least 300 numbers should be generated to allow for invalid numbers.

 

A second random digit dialing method that tends to decrease the occurrence of invalid numbers involves adding from one to three random digits to a telephone number selected from a phone directory or list of phone numbers. One first selects a number from a list of telephone numbers (a directory or list purchased from a supplier). Assume that the number 448-3047 was selected from the list. The researcher could simply add a predetermined number, say 6, to produce 448-3053; or a predetermined two-digit number, say 21, to achieve 448-3068; or even a three-digit number, say 112, to produce 448-3159. Each variation of the method helps to eliminate many of the invalid numbers produced in pure random number generation, since telephone companies tend to distribute telephone numbers in series, or blocks. In this example, the block 30— is in use, and there is a good chance that random add-ons to this block will be residential telephone numbers.

 

As indicated here, random number generation is possible via a variety of methods. However, two rules are always applicable: (1)each unit or subject in the population must have an equal chance of being selected, and (2) the selection procedure must be free from subjective intervention by the researcher. The purpose of random sampling is to reduce sampling error; violating random sampling rules only increases the chance of introducing such error into a study.

 

Similar in some ways to simple random sampling is a procedure called systematic sampling, in which every X subject or unit is selected from a population. For example, to get a sample of 20 from a population of 100, or a sampling rate of 1/5, a researcher randomly selects a starting point and a sampling interval. Thus, if the number 11 is chosen, the sample will include the 20 subjects or items numbered 11, 16, 21, 26, and so on. To add further randomness to the process, the researcher may randomly select both the starting point and the interval. For example, an interval of 11 together with a starting point of 29 would generate the numbers 40, 51, 62, 73, and so on.

 

A) Advantages

  1. Detailed knowledge of the population is not required.

  2. External validity may be statistically inferred.

  3. A representative group is easily obtainable.

  4. The possibility of classification error is eliminated.

B) Disadvantages

  1. A list of the population must be compiled.

  2. A representative sample may not result in all cases.

  3. The procedure can be more expensive than other methods.

 

 

3.4.2 Systematic Sample

Systematic samples are frequently used in social research. They often save time, resources, and effort when compared to simple random samples. In fact, since the procedure so closely resembles a simple random sample, many researchers consider systematic sampling equal to the random procedure. The method is widely used in selecting subjects from lists such as telephone directories, Broadcasting/Cdblecasting Yearbook, and Editor & Publisher.

 

The degree of accuracy of systematic sampling depends on the adequacy of the sampling frame, or a complete list of members in the population. Telephone directories are inadequate sampling frames in most cases, since not all phone numbers are listed, and some people do not have telephones at all. However, lists that include all the members of a population have a high degree of precision. Before deciding to use systematic sampling, one should consider the goals and purpose of a study, as well as the availability of a comprehensive list of the population. If such a list is not available, systematic sampling is probably ill-advised.

 

One major problem associated with systematic sampling is that the procedure is susceptible to periodicity; that is, the arrangements or order of the items in the population list may bias the selection process. For example, consider the problem mentioned earlier of analyzing television programs to determine how the elderly are portrayed. Quite possibly, every 10th program listed may have been aired by Channel 1; the result would be a nonrepresentative sampling of the three networks.

 

Periodicity also causes problems when telephone directories are used to select samples. The alphabetical listing does not allow each person or household an equal chance of being selected. One way to solve the problem is to cut each name from the directory, place them in a "hat," and draw names randomly. Obviously, this would take days to accomplish and is not a real alternative. An easier way to use a directory is to tear the pages loose, mix them up, randomly select pages, and then randomly select names. Although this procedure doesn't totally solve the problem, it is generally accepted when simple random sampling is impossible. If periodicity is eliminated, systematic sampling can be an excellent sampling methodology.

 

A) Advantages

  1. Selection is easy.

  2. Selection can be more accurate than in a simple random sample.

  3. The procedure is generally inexpensive.

 

B) Disadvantages

  1. A complete list of the population must be obtained.

  2. Periodicity may bias the process.

 

3.4.3 Stratified Sample

 

Although a simple random sample is the usual choice in most research projects, some researchers don't wish to rely on randomness. In some projects, researchers want to guarantee that a specific sub sample of the population is adequately represented. No such guarantee is possible using a simple random sample. A stratified sample is the approach used when adequate representation from a sub sample is desired. The characteristics of the sub sample (strata or segment) may include almost any variable: age, sex, religion, income level, or even individuals who listen to specific radio stations or read certain magazines. The strata may be defined by an almost unlimited number of characteristics; however, each additional variable or characteristic makes the sub sample more difficult to find. Therefore, incidence drops.

 

Stratified sampling ensures that a sample is drawn from a homogeneous subset of the population, that is, from a population with similar characteristics. Homogeneity helps researchers to reduce sampling error. For example, consider a research study on subjects' attitudes toward two-way, interactive cable television. The investigator, knowing that cable subscribers tend to have higher achievement levels, may wish to stratify the population according to education. Before randomly selecting subjects, the researcher divides the population into three levels: grade school, high school, and college. Then, if it is determined that 10% of the population completed college, a random sample proportional to the population should contain 10% who meet this standard. The stratified sampling ensures the proper representation of the stratification variables to enhance representation of other variables related to them. Taken as a whole, then, a stratified sample is likely to be more representative on a number of variables than a simple random sample.

 

Stratified sampling can be applied in two different ways. Proportionate stratified sampling includes strata with sizes based on their proportion in the population. If 30% of the population is adults (18 – 24 years), then 30% of the total sample will be subjects in this age group. This procedure is designed to give each person in the population an equal chance of being selected. Disproportionate stratified sampling is used to over sample or over represent a particular stratum. The approach is used basically because the stratum is considered important for some reason: marketing, advertising, or other similar reasons. For example, a radio station that targets 25- to 54-year-old individuals may have ratings problems with the 25- to 34-year-old group. In a telephone study of 500 respondents, the station management may wish to have the sample represented as: years old, 70% 25-34, 20% 35-49, and 10% 50-54. This distribution would allow researchers to break the 25-34 group in smaller groups such as males, females, fans of specific stations, and other subcategories and still have reasonable sample sizes.

 

A) Advantages

1. Representativeness of relevant variables is ensured.

2. Comparisons can be made to other populations.

3. Selection is made from a homogeneous group.

4. Sampling error is reduced.

 

B) Disadvantages

1. Knowledge of the population prior to selection is required.

2. The procedure can be costly and time- consuming.

3. It can be difficult to find a sample if incidence is low.

4. Variables that define strata may not be relevant.

 

3.4.4 Cluster Sample

 

The usual sampling procedure is to select one unit or subject at a time. But this requires the researcher to have a complete list of the population. In some cases there is no way to obtain such a list. One way to avoid this problem is to select the sample in groups or categories; this procedure is known as cluster sampling. For example, analyzing magazine readership habits of people in the state of Wisconsin would be time-consuming and complicated if individual subjects were randomly selected. With cluster sampling, one can divide the state into districts, counties, or zip code areas and select groups of people from these areas.

 

Cluster sampling creates two types of error: in addition to the error involved in defining the initial clusters, errors may arise in selecting from the clusters. For example, a zip code area may comprise mostly residents of a low socio-economic status who are unrepresentative of the remainder of the state; if selected for analysis, such a group may confound the research results. To help control such error, it is best to use small areas or clusters, both to decrease the number of elements in each cluster and to maximize the number of clusters selected.

 

In many nationwide studies, researchers use a form of cluster sampling called multistage sampling, in which individual households or persons are selected, not groups. Figure 3.1 demonstrates a four-stage sequence for a nationwide survey. First, a cluster of counties (or another specific geographic area) in the United States is selected. This cluster is narrowed by randomly selecting a county, district, or block group within the principal cluster. Next, individual blocks are selected within each area. Finally, a convention such as "the third household from the northeast corner" is established, and then the individual households in the sample can be identified by applying the selection formulation the stages just described.

 

In many cases researchers also need to randomly select an individual in a given household. In most cases researchers cannot count on being able to interview the person who happens to answer the telephone. Usually demographic quotas are established for a research study, which means that a certain percentage of all respondents must be of a certain sex or age. In this type of study, researchers determine which person in the household should answer the questionnaire by using a form of random numbers table.

Figure 3.1: Four-stage sequence for a nationwide survey

 

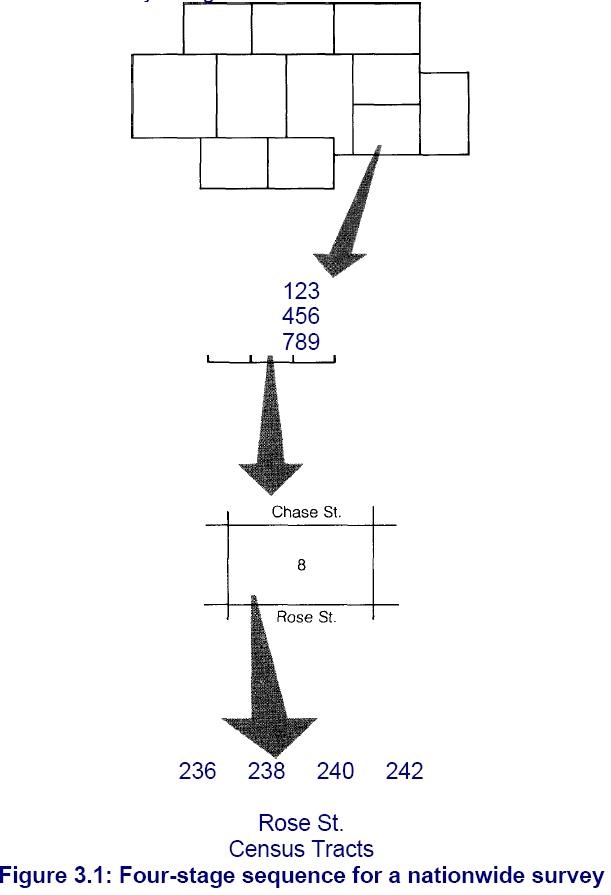
To get a random selection of individuals in the selected households, the interviewer simply asks each person who answers the telephone, "How many people are there in your home who is aged 12 or older?" If the first respondent answers "Five," the interviewer asks to speak to the fifth oldest (the youngest in this case) person in the home. Each time a call is completed, the interviewer checks off on the table the number representing the person questioned. If the next household called also had five family members, the interviewer would move to the next number in the 5 column and ask to talk to the third oldest person in the home.

The same table can be used to select respondents by sex. That is, the interviewer could ask, "How many males who are age 12 or older live in your home?" The interviewer could then ask for the "nth" oldest male, or female, according to the requirements of the survey.

 

Since media are complex systems, researchers frequently encounter complicated sampling methods. These are known as hybrid situations. Consider some researchers attempting to determine the potential for videotext distribution of a local newspaper to cable subscribers. This problem requires investigating readers and nonreaders of the newspaper as well as cable subscribers and nonsubscribers. The research, therefore, requires random sampling from the following four groups:

 

Group A      Subscribers/Readers

Group B      Subscribers/Nonreaders

Group C      Nonsubscribers/Readers

Group D      Nonsubscribers/Nonreaders

 

Researchers must identify each subject as belonging to one of these four groups. If three variables were involved, sampling from eight groups would be required, and so on. In other words, researchers are often faced with very complicated sampling situations that involve numerous steps.

 

A) Advantages

  1. Only part of the population need to be enumerated.

  2. Costs are reduced if clusters are well defined.

  3. Estimates of cluster parameters are made and compared to the population.

 

 

B) Disadvantages

  1. Sampling errors are likely.

  2. Clusters may not be representative of the population.

  3. Each subject or unit must be assigned to a specific cluster.

 

3.5 Sample Size

Determining an adequate sample size is one of the most controversial aspects of sampling. How large must a sample be to provide the desired level of confidence in the results? Unfortunately, there is no simple answer. There are suggested sample sizes for various statistical procedures, but no single sample size formula or method is available for every research method or statistical procedure. For this reason, it is advisable to consult sampling texts for information concerning specific techniques.

 

The size of the sample required for a study depends on at least one or more of the following seven points: (1) project type, (2) project purpose, (3) project complexity, (4) amount of error willing to be tolerated, (5) time constraints, (6) financial constraints, and (7) previous research in the area. Research designed as a preliminary investigation to search for general indications generally does not require a large sample. However, projects intended to answer significant questions (those designed to provide information for decisions involving large sums of money or decisions that may affect people's lives) require high levels of precision and, therefore, large samples.

 

A few general principles are used to guide researchers in determining an acceptable sample size. These suggestions are not based on mathematical or statistical theory, but they should provide a starting point in most cases.

 

  1. A primary consideration in determining sample size is the research method used. Focus groups (Chapter 7) use samples of 6-12 people, but the results are not intended to be generalized to the population from which the respondents were selected. Samples of 25-50 are commonly used for pretesting measurement instruments, pilot studies, and for studies conducted only for heuristic value.

  2. A sample of 100 subjects per demographic group (such as adults 18 - 24 years old) is often used by researchers. This base figure is used to "back in" to a total sample size. For example, assume a researcher is planning to conduct a telephone study with adults 18 - 54. Using the normal mass media age spans of 18 - 24, 25 - 34, 35 - 44, and 45 - 54, the researcher would probably consider a total sample of 400 as satisfactory (100 per age group, or "cell"). However, the researcher may also wish to investigate the differences in opinions/attitudes among men and women, which produces a total of eight different demographic cells. In this case, a sample of 800 would probably be used — 100 for each of the cell possibilities.

  3. Sample size is almost always controlled by cost and time. Although researchers may wish to use a sample of 1,000 for a survey, the economics of such sample are usually prohibitive. Research with 1,000 respondents can easily exceed $50,000. Most research work is conducted using a sample that conforms to the project's budget. If a small sample is forced on a researcher by someone else (a client or project manager), the results must be interpreted accordingly — that is, with caution regarding the generalization of results.

  4. Multivariate studies always require larger samples than univariate studies because they involve the analysis of multiple response data (several measurements on the same subject).One guideline recommended for multivariate studies is: 50 = very poor;

  5. 100 = poor; 200 = fair; 300 = good; 500 = very good; 1,000 = excellent. Other researchers suggest using a sample of 100 plus 1 subject for each dependent variable in the analysis.

  6. Researchers should always select a larger sample than is actually required for a study, since mortality must be compensated for. Subjects drop out of research studies for one reason or another, and allowances must be made for this in planning the sample selection. Subject mortality is especially prevalent in panel studies, where the same group of subjects is tested or measured frequently over a long period of time. In most cases, researchers can expect from 10% to 25% of the sample to drop out of a study before it is completed.

  7. Information about sample size is available in published research. Consulting the work of other researchers provides a base from which to start. If a survey is planned and similar research indicates that a representative sample of 400 has been used regularly with reliable results, a sample larger than 400 may be unnecessary.

  8. Generally speaking, the larger the sample used the better. However, a large unrepresentative sample is as meaningless as a small unrepresentative sample, so researchers should not consider numbers alone. Quality is always more important in sample selection than mere size.

3.6 Sampling Error

Since researchers deal with samples from a population, there must be some way for them to compare the results of (or make inferences about) what was found in the sample to what exists in the target population. The comparison allows researchers to determine the accuracy of their data and involves the computation of error. All researches involve error: sampling error, measurement error, and random error (also called unknown or uncontrollable error). Sampling error is also known as standard error. The different sources of error are additive. That is, total error is the sum of the three different sources. This section discusses sampling error in mass media research.

 

Sampling error occurs when measurements taken from a sample do not correspond to what exists in the population. For example, assume we wish to measure attitudes toward a new television program by 18- to 24-year-old viewers in Denver, Colorado. Further assume that all the viewers produce an average score of 6 on a 10-point program appeal measurement scale. Some viewers may dislike the program and rate the show a 1, 2 or 3, some find it mediocre and rate it 4, 5, 6, or 7, whereas the remaining viewers consider the show one of their favorites and rate it an 8, 9, or 10. The differences among the 18- to 24-year-old viewers provide an example of how sampling error may occur. If we asked each viewer to rate the show in a separate study and each one rated the program a 6, then no error exists. However, an error-free sample is unlikely.

 

Respondent differences do exist; some dislike the program and others like it. Although the average program rating is 6 in the hypothetical example, it is possible to select a sample from the target population that does not match the average rating. A sample could be selected that includes only viewers who dislike the program. This would misrepresent the population because the average appeal score would be lower than the mean score. Computing the rate of sampling error allows researchers to have an idea concerning the risk involved in accepting research findings as "real."

 

Computing sampling error is appropriate only with probability samples. Sampling error cannot be computed in research using non-probability samples because everyone did not have an equal chance of being selected. This is one reason why nonprobability samples are used only in preliminary research or in studies where error rates are not considered important.

 

Sampling error computations are essential in research and are based on the concept of the central limit theorem. In its simplest form, the theorem states that the sum of a large number of independent and identically distributed random variables (or sampling distributions), has an approximate normal distribution. A theoretical sampling distribution is the set of all possible samples of a given size. This distribution of values is described by a bell-shaped curve, or normal curve (also known as a Gaussian distribution, after German mathematician and astronomer Karl F. Gauss who used the concept to analyze observational errors). The normal distribution is important in computing sampling error because sampling errors (a sampling distribution) made in repeated measurements tend to be normally distributed.

 

Computing standard error is a process of determining, with a certain amount of confidence, the difference between a sample and the target population. Error occurs by chance, or through some fault of the research procedure. However, when probability sampling is used, the incidence of error can be determined because of the relationship between the sample and the normal curve. A normal curve is symmetrical about the mean or midpoint, which indicates that an equal number of scores lie on either side of the midpoint.

 

In every normal distribution, the standard deviation defines a standard unit of distance from the midpoint of the distribution to the outer limits of the distribution. These standard deviation interval unit(values) are used in establishing a confidence interval that is accepted in a research project. In addition, the standard deviation units indicate the amount of standard error. For example, using an interval (confidence interval) of + or — one standard deviation unit — 1 standard error — says that the probability is that 68% of the sample selected from the population will produce estimates within that distance from the population value (one standard deviation unit).

 

3.6.1 Computing Standard Error

 

The essence of statistical hypothesis testing is to draw a sample from a target population, compute some type of statistical measurement, and compare the results to the theoretical sampling distribution. The comparison determines the frequency with which sample values of a statistic are expected to occur.

 

The expected value of a statistic is the mean of the sampling distribution. The standard error is the standard deviation of the sampling distribution. There are several ways to compute standard (sampling) error, but no single method is appropriate for all sample types or for all situations. In addition, error formulas vary in complexity. One error formula, designed for estimating audience sizes during certain time periods or for certain programs and for measuring cumulative audiences uses the standard error of a percentage derived from a simple random sample. If the sample percent is designated as p, the size of the sample as n, and the estimated or standard error of the sample percentage as SE(p), the formula is:

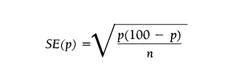
Suppose a random sample of 500 households produces a rating (or estimate of the percentage of viewers) of 20 for a particular show. This means that 20% of those households were tuned in to that channel at that time. The formula can be used to calculate the standard error as follows:

 

 

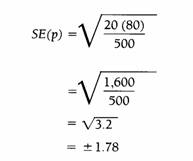
That is, the rating of 20 computed in the survey is subject to an error of ± 1.78 points; the actual rating could be as low as 18.22 or as high as 21.78.

 

Standard error is directly related to sample size. The error figure improves as the sample size is increased, but in decreasing increments. Thus, an increase in sample size does not provide a big gain. As can be seen, even with a sample of 1,500, the standard error is only .75 better than with a sample of 500 computed above. A researcher would need to determine whether the increase in time and expense caused by an additional 1,000 subjects would justify such a proportionally small increase in precision.

 

The following table shows the amount of error at the 95% confidence level for measurements that contain dichotomous variables (such as "yes/ no"). For example, with a sample of 1,000 and a 30% "yes" response to a question, the probable error due to sample size alone is ± 2.9. This means that we are 95% sure that our values for this particular question fall between 27.1% and 32.9%. Sampling error is an important concept in all research areas because it provides an indication of the degree of accuracy of the research.

 

Research studies published by large audience measurement firms such as Arbitron and A. C. Nielsen are required by the Electronic Media Ratings Council to include simplified charts to assist in determining sampling error. In addition, each company provides some type of explanation about error, such as the Arbitron statement contained in every ratings book:

Arbitron estimates are subject to statistical variances associated with all surveys using a sample of the universe. . . . The accuracy of Arbitron estimates, data and reports and their statistical evaluators cannot be determined to any precise mathematical value or definition.

 

Statistical error due to sampling is found in all research studies. Researchers must pay specific attention to the potential sources of error in any study. Producing a study riddled with error is tantamount to never having conducted the study at all. If the magnitude of error was subject to accurate assessment, researchers could simply determine the source of error and correct it. Since this is not possible, however, they must accept error as part of the research process, attempt to reduce its effects to a minimum, and remember always to interpret their results with regard to its presence.

3.7 Sample Weighting

In an ideal research study, a researcher should have enough respondents or subjects with the required demographic, psychographic (why people behave in specific ways), or lifestyle characteristic. The ideal sample, however, is rare, due to the time and budget constraints of most research. Instead of canceling a research project because of sampling inadequacies, most researchers utilize a statistical procedure known as weighting, or sample balancing. That is, when subject totals in given categories do not reach the necessary population percentages, subjects' responses are multiplied (weighted) to allow for the shortfall. A single subject's responses may be multiplied by 1.3, 1.7, 2.0, or any other figure to reach the predetermined required level.

 

Subject weighting is a controversial data manipulation technique, especially in the area of broadcast ratings. The major question is just how much one subject's responses can be weighted and still be representative.